Silas & Müllensiefen (2023) online supplement • musicassessr

1 Short melodic excerpts from pop songs used as materials in the study

No.	Song	Composer/Interpreter	Genre/Meter	Tempo
1	Children Of The Night	R. Marx	Pop 4/4	75
2	Climb Up	N. Sedaka	R´n´R 4/4	120
3	Cold Cold Heart	M. Pellow	Pop 4/4	80
4	Do You Want To Dance?	R. Freeman	R´n´R 4/4	100
5	Du gehörst zu mir	J. Heider	Schlager 4/4	120
6	Longer	D. Fogelberg	Pop-Ballade 4/4	80
7	Oh Carol	N. Sedaka	Pop-Ballade 4/4	140
8	Take Good Care	C. King	Ballade 4/4	120
9	The Sky Is Crying	M. Levy	Blues 12/8	60
10	You Are My Destiny	P. Anka	Schlager 12/8	85
11	Goodbye My Love Goodbye	M. Panas / D. Roussos	Schlager 4/4	114
12	Enjoy Your Life	Funky Be	HipHop 4/4	85
13	Love Is Like A Rainbow	T. Anders	Disco-Pop 4/4	155
14	Let Me Be Your Only One	Funky Be	HipHop 4/4	100

2 An example of one melody from each pop song.

2.0.1 Melody No. 1, Children of the Night, R.Marx

2.0.2 Melody No. 2, Climb Up, N.Sedaka

2.0.3 Melody No. 3, Cold Cold Heart, M.Pellow

2.0.4 2.1.4: Melody No. 4, Do You Want To Dance?, R. Freeman

2.0.5 Melody No. 5, Du gehörst zu mir, J. Heider

2.0.6 Melody No. 6, Longer, D.Fogelberg

2.0.7 Melody No. 7, Oh Carol, N. Sedaka

2.0.8 Melody No. 8, Take Good Care, C. King

2.0.9 Melody No. 9, The Sky is Crying, M.Levy

2.0.10 Melody No. 10, You Are My Destiny, P. Anka

2.0.11 Melody No. 11, Goodbye My Love Goodbye, M. Panas / D. Roussos

2.0.12 Melody No. 12, Enjoy Your Life, Funky Be

2.0.13 Melody No. 13, Love Is Like A Rainbow, T. Anders

2.0.14 Melody No. 14, Let Me Be Your Only One, Funky Be

2.1 Description and distribution of melodic features

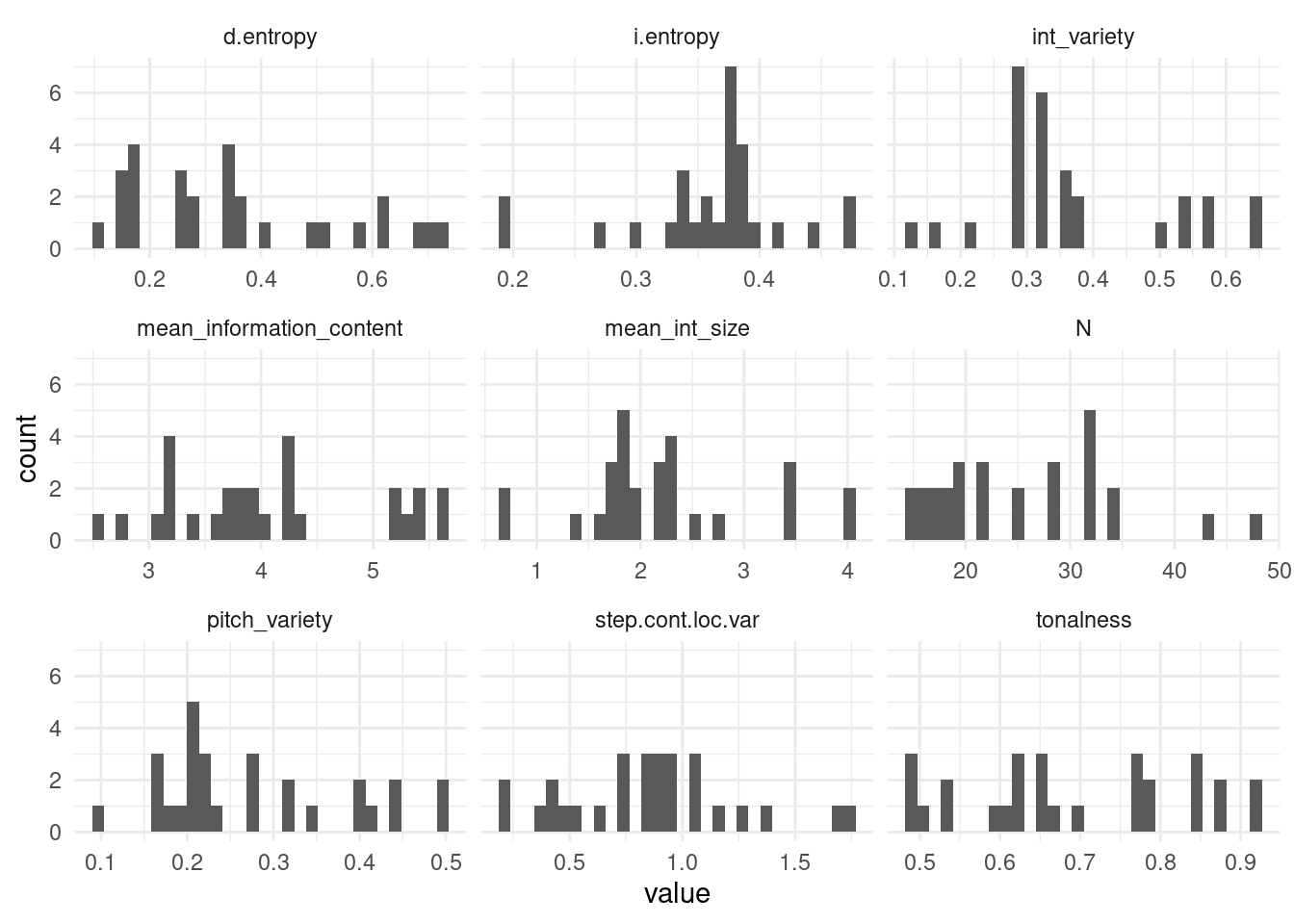
2.2 Melodic feature summary statistics

Table 2.1: Melodic feature summary statistics. Note, some are not used in our modelling, but are here to show other properties of the melodies.
Feature	Mean	SD	Coefficient of Variation
d.entropy	0.36	0.19	0.53
step.cont.loc.var	0.86	0.38	0.44
pitch.variety	0.28	0.11	0.40
mean.int.size	2.21	0.84	0.38
int.variety	0.37	0.13	0.37
N	25.39	8.66	0.34
mean.information.content	4.07	0.89	0.22
tonalness	0.69	0.14	0.20
i.entropy	0.36	0.06	0.18

3 Questionnaire items

Variable	Question	Response Format
chorusin	Do you sing in a choir?	Yes/No
singinstr:	Have you ever received singing instructions?	Yes/No
yearsins	For how many years have you been playing an instrument or making music?	__years
musmakpa	During your most active musical phase how many hours per week did you make music (practice+rehearsal+gigs+lessons+playing+etc.)	__hours/week
paidless	For how many months have you received paid instrumental or singing lessons?	__ months
paidgigs	How many gigs have you played that you have been paid for?	___gigs
gigs	Overall, how many gigs have you played in front of an audience in your life?	___gigs

3.1 Factor loadings for mixed type variables based on questionnaire items

Variable	Loading	h2	u2
chorusin	0.70	0.49	0.51
singinstr	0.46	0.21	0.79
yearsins	0.82	0.67	0.33
musmakpa	0.77	0.59	0.41
paidless	0.65	0.42	0.58
paidgigs	0.66	0.44	0.56
gigs	0.69	0.48	0.52

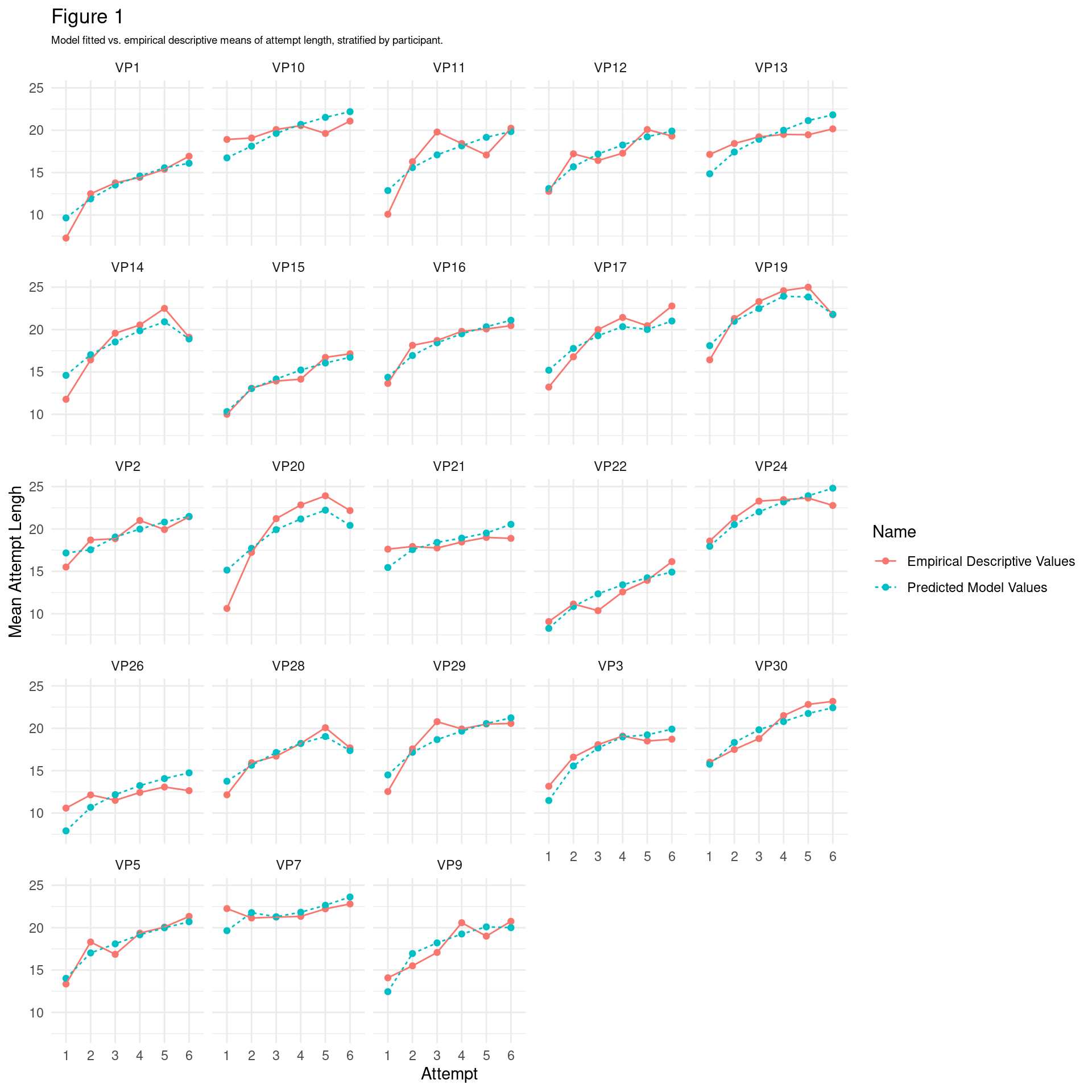
4 Average by-participant performance across attempts

4.1 Average by-participant development of attempt length

4.2 Average by-participant development of opti3

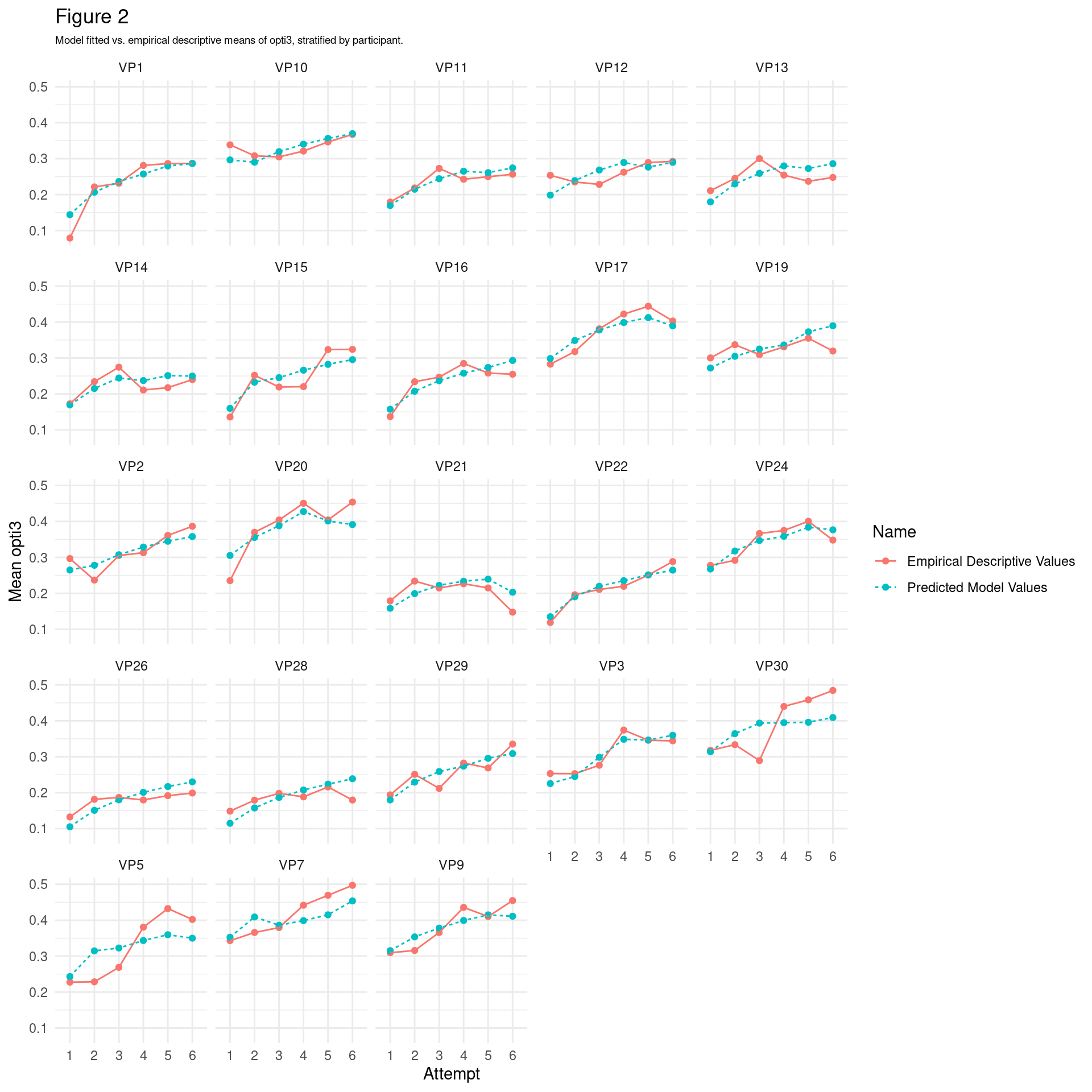
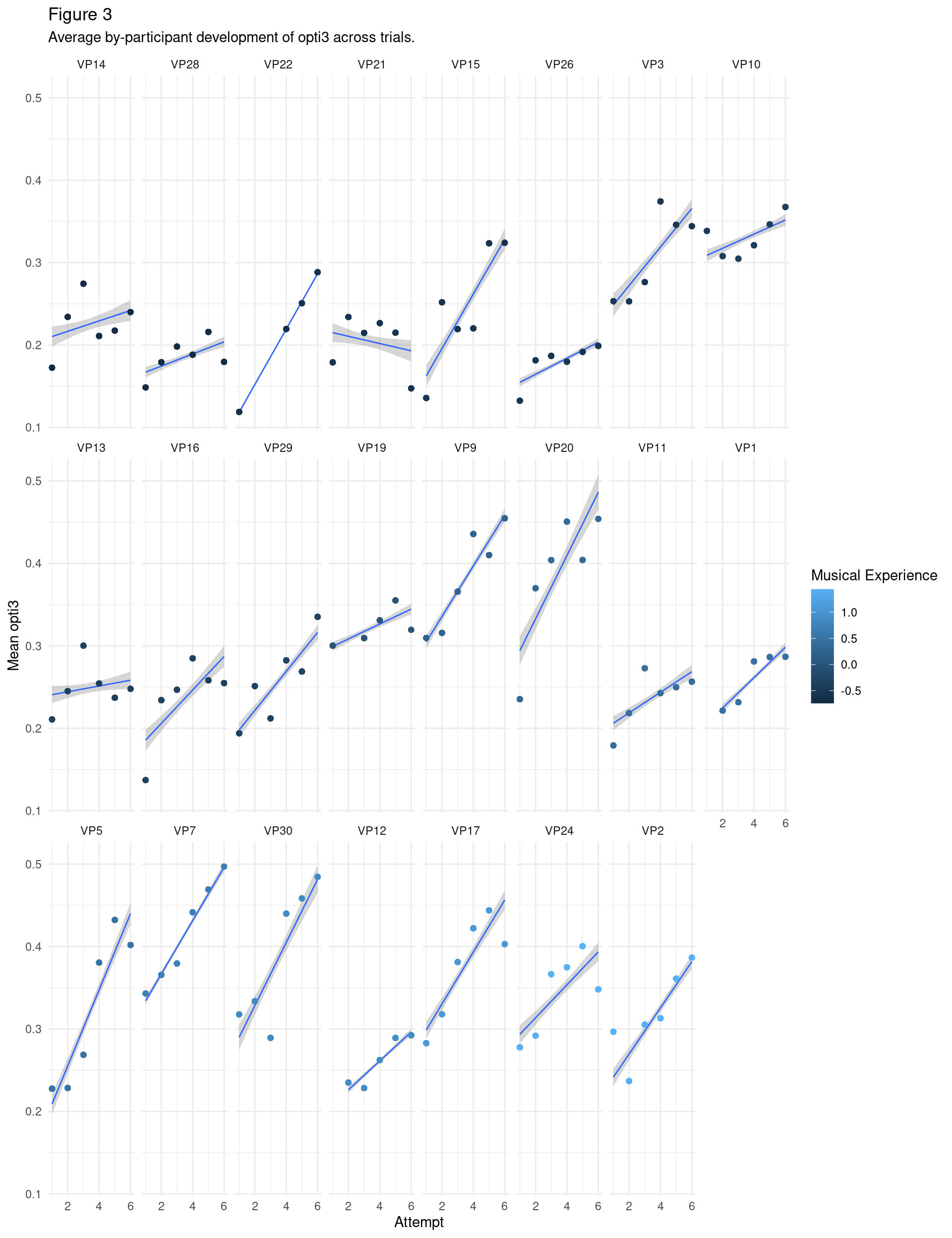
Another way of visualising differences in performance is at the level of participant, coloured and ordered by level of musical experience. This is useful since it invokes no false dichotimisations and preserves the actual unit of participant (however, note that participant-level effects are captured by our mixed effects models).

As shown in Figure 2, participants seem to have vastly different slopes. The bottom right, lighter blue, higher musical experience participants (e.g., VP5, VP7, VP30, VP12, VP17, VP24, VP2) seem to have steeper slopes than the lower musical experience participants in the top left, darker coloured (VP14, VP28, VP21), suggesting that higher musical experience is related to quicker learning. However, note that this pattern is not the same for everyone e.g., VP22 has a steep slope, but scores low on musical experience

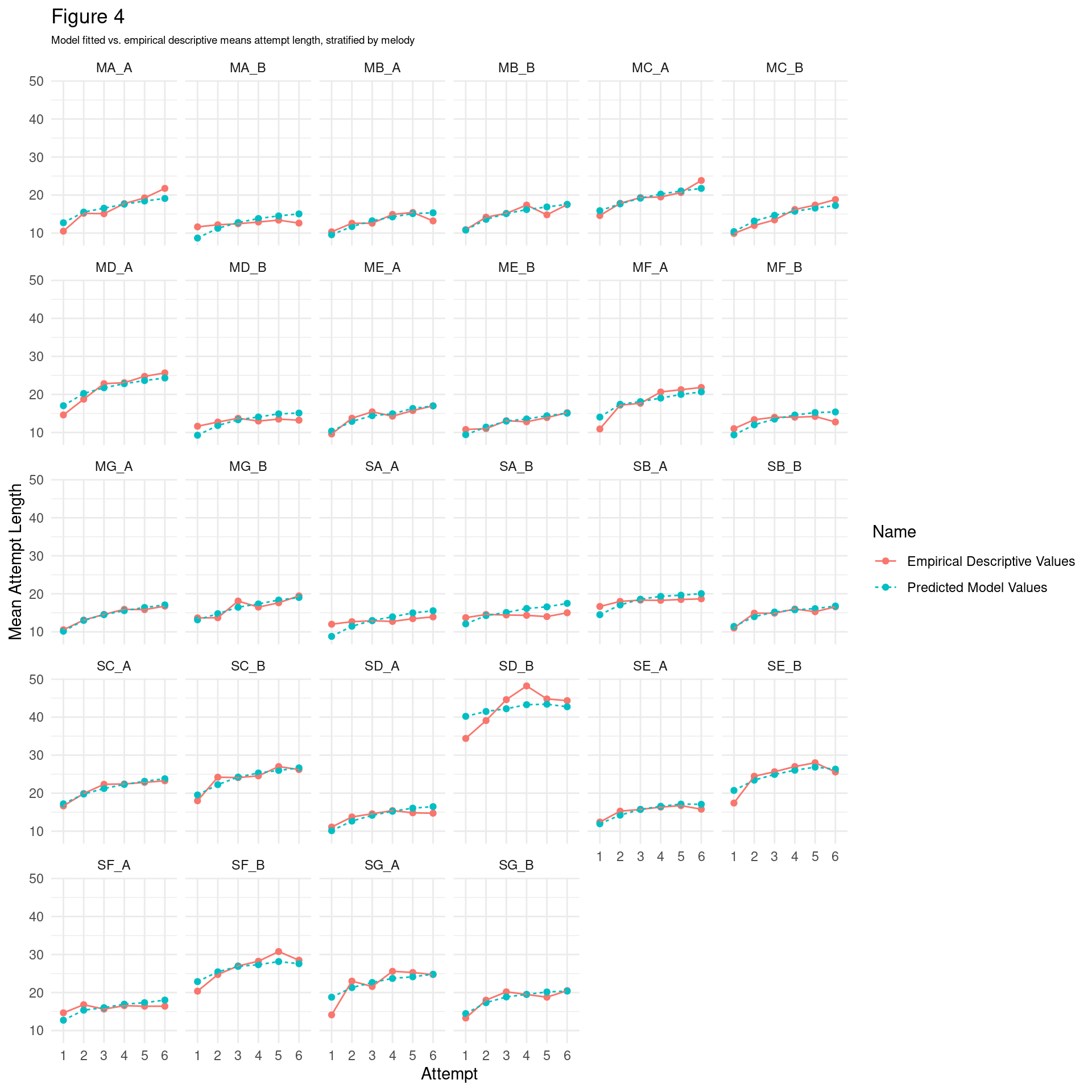
5 Average by-melody performance across attempts

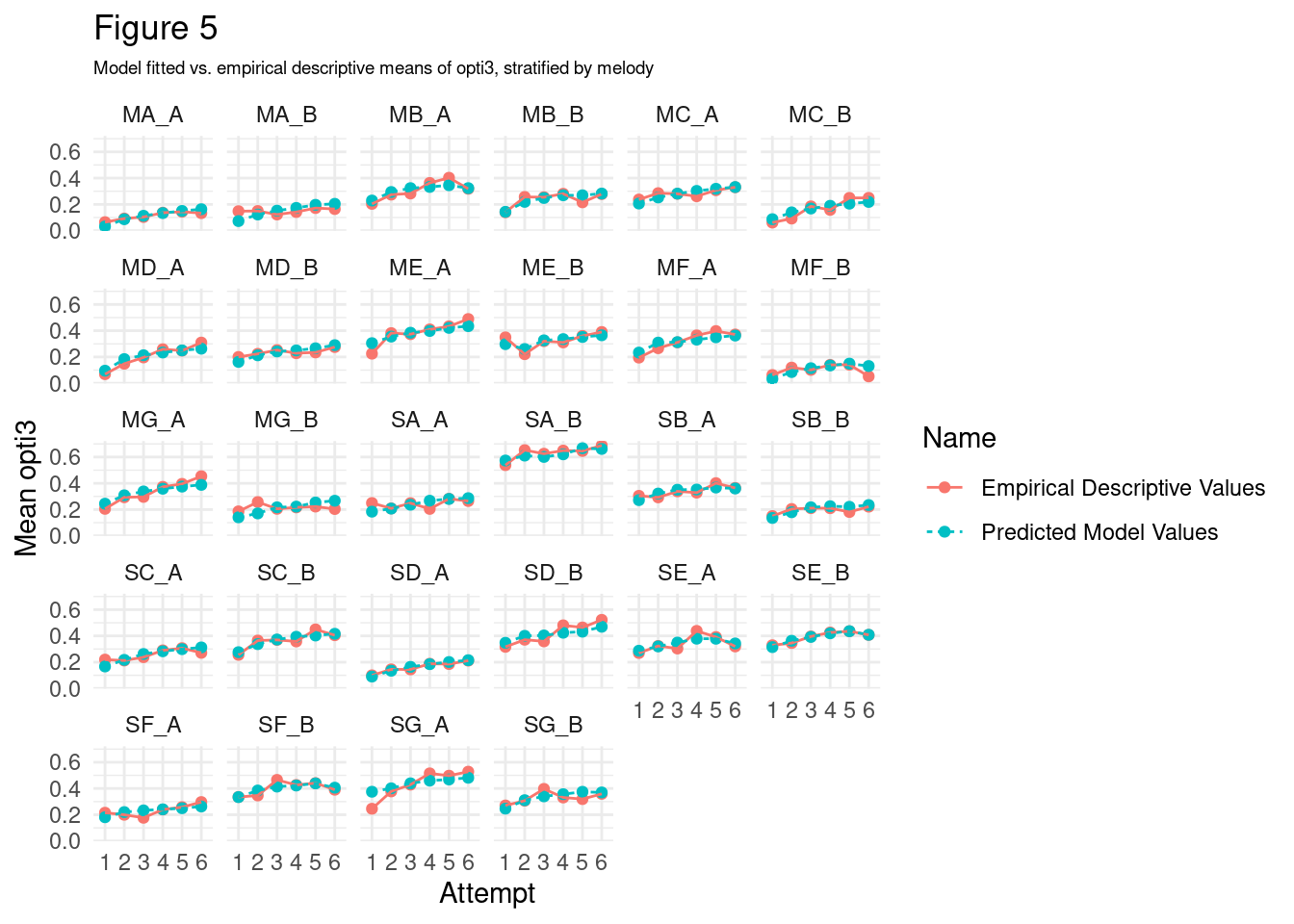
5.1 Average by-melody development of attempt length

5.2 Average by-melody development of opti3

Melody SA_B appears to be the easiest melody to recall (mean opti3 across all trials = 0.61), whereas MF_B appears most difficult to recall (mean opti3 across all trials = 0.11). This shows that there can be substantial variation in the difficulty of each melody.

6 Linear vs. Non-Linear Models of dependent variables

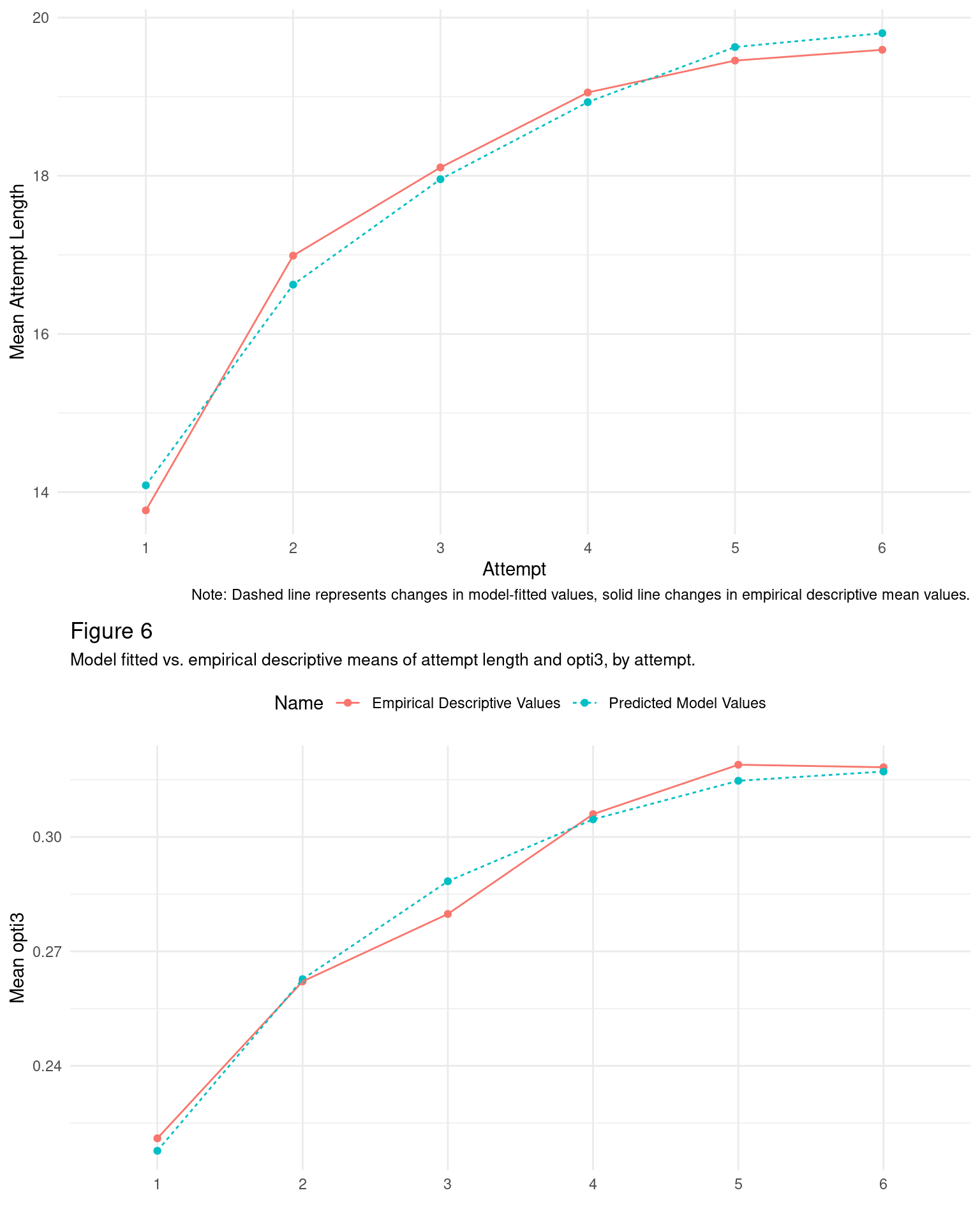
We proceed by using the log attempt as numeric predictor, owing to the observed non-linearities in both opti3 and attempt length across attempt. A comparison of linear vs non-linear models is shown below.

6.1 Linear model of attempt length across repeated attempts

Table 6.1: A linear model of attempt length regressed onto attempt with melody item, participant and the interaction between melody item and participant as random effects. Note that the linear model is not taken forward.
Term	\(\hat{\beta}\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	13.72	[11.12, 16.32]	10.34	38.29	< .001
Attempt2	3.26	[2.59, 3.92]	9.63	1449.39	< .001
Attempt3	4.54	[3.88, 5.20]	13.45	1452.67	< .001
Attempt4	5.58	[4.91, 6.25]	16.30	1457.44	< .001
Attempt5	6.10	[5.43, 6.78]	17.62	1458.23	< .001
Attempt6	6.74	[6.04, 7.43]	19.01	1458.66	< .001

Figure 6 shows that the use of the log attempt as predictor is justified, capturing the systematic non-linear pattern generally well.

6.2 Linear model of mean similarity scores (opti3) across repeated attempts

Table: (#tab:unnamed-chunk-30)

Table 6.2: A linear model of opti3 regressed onto attempt with melody item, participant and the interaction between melody item and participant as random effects. Note that the linear model is not taken forward.
Term	\(\hat{\beta}\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	0.22	[0.17, 0.27]	7.96	44.96	< .001
Attempt2	0.05	[0.03, 0.06]	5.02	1441.05	< .001
Attempt3	0.07	[0.05, 0.09]	7.36	1444.00	< .001
Attempt4	0.10	[0.08, 0.12]	10.58	1448.03	< .001
Attempt5	0.12	[0.10, 0.14]	12.47	1448.89	< .001
Attempt6	0.13	[0.11, 0.15]	13.23	1449.24	< .001

7 Diagnostic statistics for models with all features in (partial R-squared and variance inflation factor values)

7.1 With attempt length as dependent variable

Table 7.1: Variation inflation factor (VIF) values for model with all features in and attempt length as dependent variable
Predictor	VIF
condition	1.63
log(attempt_numeric)	1.00
N	4.59
tonalness	2.22
i.entropy	4.50
step.cont.loc.var	5.46
d.entropy	1.84
mean_information_content	4.58

Table 7.2: Partial R-Squared values for model with all features in and attempt length as dependent variable
Effect	F	v1	v2	ncp	Rsq	upper.CL	lower.CL
Model	188.68	8.00	1,763.00	1,509.42	0.46	0.49	0.43
log(attempt_numeric)	203.38	1.00	1,763.00	203.38	0.10	0.13	0.08
N	93.27	1.00	1,763.00	93.27	0.05	0.07	0.03
conditionS	84.95	1.00	1,763.00	84.95	0.05	0.07	0.03
tonalness	72.84	1.00	1,763.00	72.84	0.04	0.06	0.02
d.entropy	62.88	1.00	1,763.00	62.88	0.03	0.05	0.02
step.cont.loc.var	32.40	1.00	1,763.00	32.40	0.02	0.03	0.01
mean_information_content	0.57	1.00	1,763.00	0.57	0.00	0.00	0.00
i.entropy	0.02	1.00	1,763.00	0.02	0.00	0.00	0.00

7.2 With opti3 as dependent variable

Table 7.3: Variation inflation factor (VIF) values for model with all features in and opti3 as dependent variable
Predictor	VIF
condition	1.58
log(attempt_numeric)	1.00
N	4.58
tonalness	2.19
i.entropy	4.46
step.cont.loc.var	5.45
d.entropy	1.78
mean_information_content	4.57

Table 7.4: Partial R-Squared values for model with all features in and opti3 as dependent variable
Effect	F	v1	v2	ncp	Rsq	upper.CL	lower.CL
Model	42.54	8.00	1,758.00	340.36	0.16	0.20	0.14
mean_information_content	139.38	1.00	1,758.00	139.38	0.07	0.10	0.05
log(attempt_numeric)	86.68	1.00	1,758.00	86.68	0.05	0.07	0.03
i.entropy	78.48	1.00	1,758.00	78.48	0.04	0.06	0.03
conditionS	72.03	1.00	1,758.00	72.03	0.04	0.06	0.02
N	35.68	1.00	1,758.00	35.68	0.02	0.03	0.01
step.cont.loc.var	2.26	1.00	1,758.00	2.26	0.00	0.01	0.00
d.entropy	0.44	1.00	1,758.00	0.44	0.00	0.00	0.00
tonalness	0.00	1.00	1,758.00	0.00	0.00	0.00	0.00

8 Counts of overall number of trials that participants utilise for multiple attempts

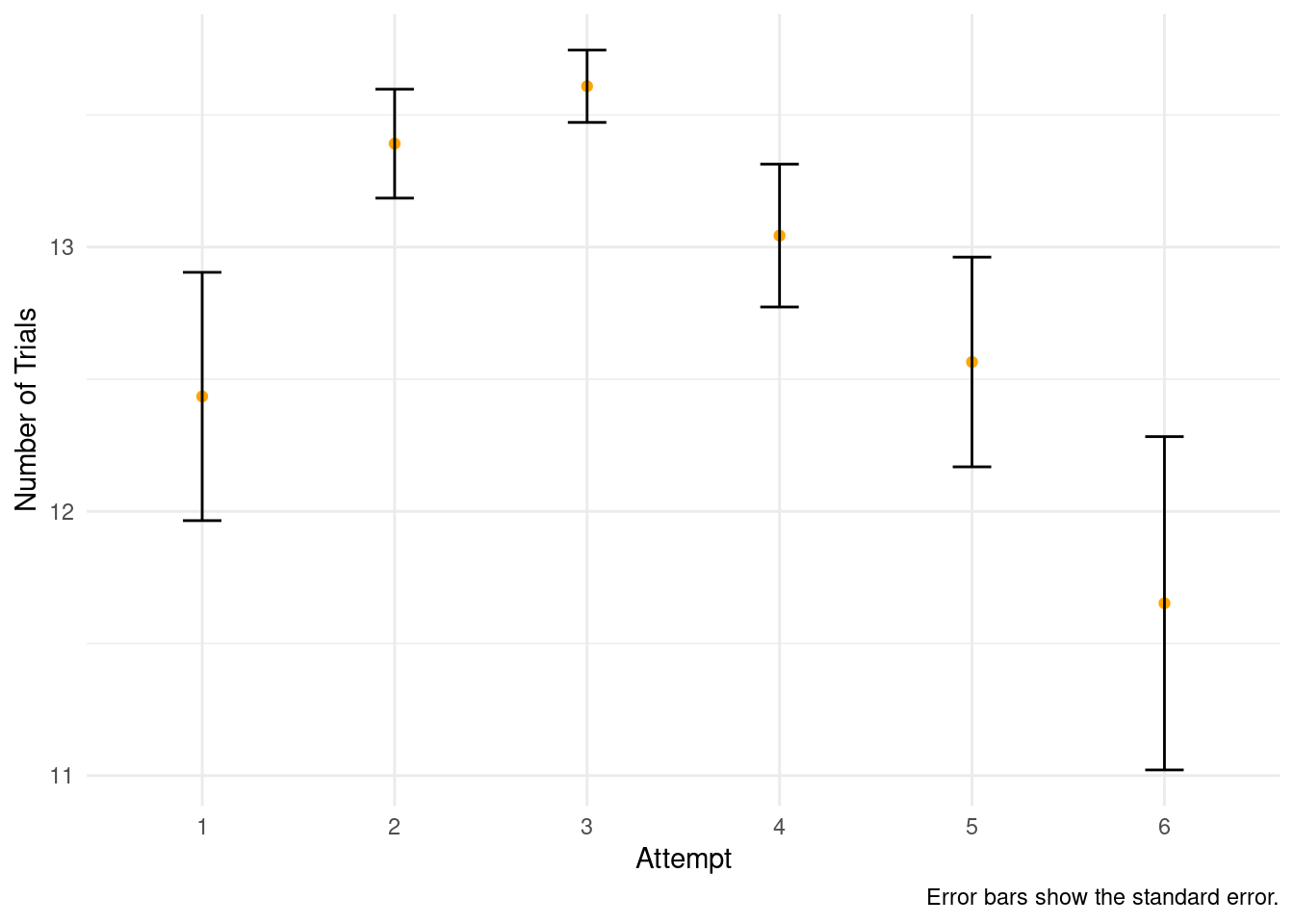
To assess whether the change across attempts depended on musical experience, we fitted a mixed effects model with trial count as the dependent variable, participant as random effect and the following fixed effects: linear terms for attempt and musical experience; an additional quadratic term for attempt; a linear interaction term for attempt and musical experience; and a quadratic interaction interaction term for musical experience. The model is presented below.

Table 8.1: Model of trial counts as a function of attempt number, musical experience and interactions
Term	\(\hat{\beta}\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	11.51	[10.24, 12.78]	17.75	131.19	< .001
Attempt numeric	1.27	[0.48, 2.07]	3.13	111	.002
Iattempt numeric^2	-0.21	[-0.32, -0.10]	-3.67	111	< .001
Musical experience	-0.51	[-2.32, 1.29]	-0.56	131.19	.579
Attempt numeric \(\times\) Musical experience	0.40	[-0.73, 1.54]	0.70	111	.486
Iattempt numeric^2 \(\times\) Musical experience	-0.07	[-0.23, 0.09]	-0.91	111	.366

9 Statistical models to support changes in similarity as a function of attempt and melody section

9.1 opti3

Table 9.1: Change in opti3 as a function of log attempt and section of sung recall (beginning, middle, end)
Predictor	\(b\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	0.09	[0.09, 0.10]	115.14	133727	< .001
Melody sectionopti3 prim	0.02	[0.02, 0.02]	24.11	133727	< .001
Melody sectionopti3 rec	0.00	[-0.01, 0.00]	-5.12	133727	< .001
Logattempt	0.02	[0.02, 0.02]	36.15	133727	< .001

9.2 ngrukkon

Table 9.2: Change in ngrukkon as a function of log attempt and section of sung recall (beginning, middle, end)
Predictor	\(b\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	0.06	[0.06, 0.06]	66.75	133727	< .001
Melody section nngrukkon prim	0.03	[0.03, 0.03]	37.07	133727	< .001
Melody section nngrukkon rec	0.00	[0.00, 0.00]	0.00	133727	.997
Logattempt	0.03	[0.03, 0.03]	52.09	133727	< .001

9.3 rhythfuzz

Table 9.3: Change in rhythfuzz as a function of log attempt and section of sung recall (beginning, middle, end)
Predictor	\(b\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	0.22	[0.21, 0.22]	391.50	142691	< .001
Melody section rrhythfuzz prim	0.00	[0.00, 0.00]	-5.17	142691	< .001
Melody section rrhythfuzz rec	-0.01	[-0.01, -0.01]	-13.43	142691	< .001
Logattempt	0.03	[0.03, 0.03]	83.45	142691	< .001

9.4 harmcore

Table 9.4: Change in harmcore as a function of log attempt and section of sung recall (beginning, middle, end)
Predictor	\(b\)	95% CI	\(t\)	\(\mathit{df}\)	\(p\)
Intercept	0.36	[0.35, 0.36]	134.19	142691	< .001
Melody section hharmcore prim	0.03	[0.02, 0.03]	11.24	142691	< .001
Melody section hharmcore rec	0.00	[0.00, 0.01]	0.13	142691	.899
Logattempt	0.02	[0.01, 0.02]	9.54	142691	< .001